On our LSAT Discussion Forum recently, I’ve been running into a recurrent question about a conditional reasoning rule. These questions revolve around a really tricky phrasing, one that has devastated test takers when it has appeared on previous LSATs. But if you can learn the idea, it takes something the test makers expect to be very difficult and turns it into something fairly easy. Plus, it’s not that tough to learn! So what is this mysterious but critically important concept?
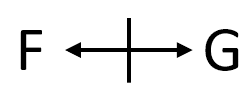
The LSAT frequently presents conditional reasoning. And, in many instances, they construct statements so that one of the conditions is positive and the other is negative. For example, you might see a Logic Game rule such as “If F is selected, then G cannot be selected.” Here, the sufficient condition is positive and the necessary condition is negative:
Readers of the LSAT Bibles or students in one of the PowerScore LSAT courses will recognize that we typically turn the above statement into the following super-statement:
This representation captures the full meaning of the initial diagram and its contrapositive (and we discuss that elsewhere in great detail, so I’ll skip that breakdown for now). What is interesting here is what is possible and impossible under this scenario. There are three possible outcomes and one impossible outcome:
1. F occurs, G does not occur
2. G occurs, F does not occur
3. Neither F nor G occurs
What is impossible is for both F and G to occur.
Thus far, everything looks fairly normal, and the vast majority of “one positive condition and one negative condition” rules that one encounters on Logic Games come in the above form. However, there is a similar rule that the test makers throw in on rare occasion, but when they do, it causes all sorts of problems (for example, see the famous December 2000 Birds in the Forest game). This tricky rule is worded in the following form: “If F is not selected, then G must be selected.” Here, the sufficient condition is negative and the necessary condition is positive:
This rule looks so similar to the previous one that it is easy to see why it would cause confusion. Both rules contain F and G and a single arrow, and there is one negative and one positive term. But, when the negative is moved over to the sufficient condition, it completely changes the meaning of the rule. Under this rule, there are also three possible outcomes and one impossible outcome:
1. F occurs, G does not occur
2. G occurs, F does not occur
3. Both F and G occur
What is impossible is for neither F nor G to occur.
The effective result of the change is that the two rules have inverse outcomes. In the first rule (F → G), you can never have both variables present, but in the second rule (F → G) you can never have both variables absent. So, when you are setting up a Logic Game, the first rule means that one of F and G (and possibly both) is always out; the second rule means that one of F and G (and possibly both) is always in. That is a huge difference in meaning in a game, and one that—if you did not get it right—would cause you to miss multiple questions (if you have the LSAT Logic Games Bible, check out the game on page 340 (the photograph game). If you mis-analyze the fourth rule in this game, you are dead).
The next LSAT isn’t that far away. I don’t know for sure that this rule will appear, but it has been used more in recent years than it had been used previously. If you can commit this rule to memory and understand how it works, then if it appears, it just might save your score.
Have any questions or comments? Please post them below!



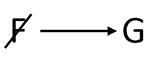
Julie says
The pictures don’t seem to be loading. Can you please fix?
thanks!
Dave Killoran says
They are updating that! It looks like there was a change in the backend and now updates for these are needed, so this may occur elsewhere for a bit. So, they used to be there but now are not, so we will get that fixed. Thanks for the notice!
Edit: this is now fully updated 🙂
Ryan says
Hi Dave,
Great post. I’ve mentioned before on the PowerScore forums that my undergrad is in computer engineering so I’ve had a lot of courses which require logic. However, it’s almost exclusively been digital logic (what my university calls digital logic, anyway) and as such I tend to think about it in terms of 1s and 0s and/or use the rules of Boolean algebra to reduce complex expressions down to logically equivalent, and much more manageable expressions.
For instance, when reasoning through the two rules presented in this post, I immediately drew a truth table to confirm my thinking was correct. In my discrete math course, I was taught that the ONLY time a conditional statement is false is when the hypothesis is true and the conclusion is false (since, P –> Q is logically equivalent to ~P or Q). Thus, the two truth tables I came up with are shown below:
F G ~G | F –> ~G
0 0 1 1
0 1 0 1
1 0 1 1
1 1 0 0
F G ~F | ~F –> G
0 0 1 0
0 1 1 1
1 0 0 1
1 1 0 1
We, of course, both got the same results. My question is, as the logic required on the LSAT is applied so differently than almost anything I’ve done in undergrad (not to mention the amount of time it takes to write out truth tables is much too long to be useful on the LSAT), is this type of thinking even beneficial for me or should I essentially forget what I’ve learned in digital logic in favor of “LSAT” logic?
I originally thought that the logic on the LSAT would be easier for me because of I’ve used logic so extensively in computer programming and digital circuit courses. Unfortunately, it’s applied so differently that I’ve found this is not the case.
Thank you,
Ryan