This is Part II of our blog series covering the emerging trend of making you labor over strangely-worded or confusing rules in LSAT Logic Games. You can read the first part of the blog here. It’s worth repeating that none these rules can be described as ambiguous, i.e. none of them are open to multiple interpretations. Indeed, each rule entails a concrete and definitive outcome.
In the second part of this blog series, we will analyze a conditional rule frequently encountered in Linear Games. This rule is particularly prone to misinterpretation:
The Victorian painting must be restored later in the week than the Renaissance painting or later in the week than the Modernist painting, but not both.
Notice that the rule has two parts.
Part One
The Victorian painting must be restored later in the week than the Renaissance painting OR later in the week than the Modernist painting.
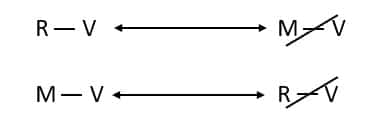
The first part of the rule has the classic form of an “either/or” statement, outlining two possible sequences—R > V or M > V—one of which must always occur. So, if the first sequence does not occur, i.e. if the Victorian painting is NOT restored later in the week than the Renaissance painting, then it must be restored later in the week than the Modernist painting:
By the contrapositive, if the Victorian painting is NOT restored later in the week than the Modernist painting, then it must be restored later in the week than the Renaissance painting:
Part Two
The Victorian painting CANNOT be restored later in the week than both the Renaissance painting and the Modernist painting
According to the second half of the rule, the two sequences outlined above CANNOT occur simultaneously. So, if the first sequence does occur, i.e. if the Victorian painting is restored later in the week than the Renaissance painting, then it CANNOT be restored later in the week than the Modernist painting:
By the contrapositive, if the Victorian painting is restored later in the week than the Modernist painting, then it CANNOT be restored later in the week than the Renaissance painting:
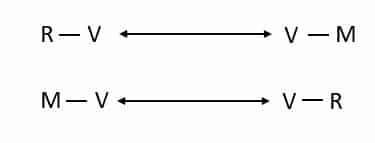
When combined, the two parts of this rule produce the following conditional relationship between the M > V and R > V sequences:
Assuming that no two paintings can be restored simultaneously, we can simplify the diagram by eliminating any negated terms:
Thus, we can create two separate, exhaustive, and mutually exclusive sequencing chains, one of which will always govern the order in which the three paintings are being restored:
This is a much simpler representation of the original rule, showing us an important inference that you may not have seen otherwise: the Victorian painting can never be the first or the last painting restored that week.
After you practice with this type of rule a few times, you can probably jump straight into creating the two sequencing chains without diagramming the original conditional statements. While there is always the danger of misinterpretation, as long as you understand the precise conditional relationship between each two pairs of sequencing rules you should not forfeit accuracy for the sake of speed. Indeed, superior conceptual understanding does not automatically entail more time spent analyzing the rule in question: on the contrary, over time, this understanding will enable you to formulate ever more quickly the concrete and definitive outcome of the rules governing the composition of variables in your game.