The last time a Circular Linear game made an appearance on an LSAT was the February 2014 exam. Unfortunately, this test is undisclosed, so we will never actually see the game. This very game is also rumored to be a “tiered circular linear” game. It involves two variable sets to be distributed around a circle. We’ll never know for sure, but such a game is not outside the realm of possibility. The following list shows every single appearance of a Circular Logic game on the test since 1991.
- June 1991, Game #1
- June 1993, Game #2
- February 1999, Game #3
- October 2003, Game #4
As you can see, Circular Linear games are exceptionally rare with a frequency rate of less than 1.5%. But they do occur! It’s better to be safe and studied than sorry. Here’s a sample scenario of a Tiered Circular Linear game. Bear in mind that since the February 2014 exam is undisclosed, we have not seen an actual copy of one in practice.
Sample Game
Known Variables
Like all circular games, this one consists of a fixed number of variables assigned to spaces evenly distributed around a circle or table. Notice that for each seat at the table we need to keep track of two attributes: age (adult vs. child) and name (F, G, H, P, R, and S). This is where the name “tiered” circular game comes from. Thankfully, the two variable sets are fixed to each other, so we don’t need to determine who is an adult or child. Using tiers may not be necessary.
Set Up a Diagram
Don’t waste your time drawing out a table. Use a “spokes” diagram instead! Represent each seat by the end of a “spoke.” Since there is an even number of individuals around the table, everyone must sit directly across from someone else. A “spokes” diagram will help you represent this idea more easily.
In Circular games with an even number of variables, rules involving opposites are particularly important. The first rule of our game is worth a closer look.
Each child sits directly across from one of the adults.
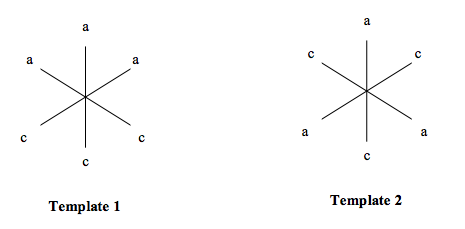
Since there are as many adults as children, we can infer that each adult sits across from a child. The seats do not have specific numbers, which is important to note. This allows us to arbitrarily place the adults and children across from each other as long as the arrangement doesn’t violate the rule. By focusing on the categorical variable set (adults/children), you will quickly realize that there are only two possible ways to distribute them around the table.
Apply the Rules
This approach restricts the variables that occupy any given seat to one of three, rather than one of six. Because the two templates are restrictive, we can examine the application of the last three rules more closely.
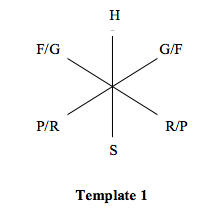
F does not sit immediately next to G.
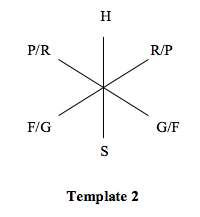
The second rule establishes that F doesn’t sit immediately next to G. Since F and G are both adults, Template 2 never violates this rule. In Template 1, however, we need to ensure that F and G never sit next to each other by placing another adult (H) between them.
Let’s look at the next rule.
P does not sit immediately next to R.
The third rule establishes that two of the children, P and R, do not sit next to each other. As with the previous rule, Template 2 never violates this rule due to the alternating arrangement in the template. For Template 1, we need to ensure that P and R aren’t immediately adjacent in Template 1. So the third child, S, must separate them.
Now onto the final rule.
H does not sit immediately next to S.
The last rule forbids S (a child) from sitting immediately next to H (an adult). In Template 1, H and S sit directly across from each other, so clearly this isn’t a problem. However, Template 2 needs to ensure it doesn’t violate this rule, as well. If S cannot sit next to H, the two children sitting next to H must be none other than P and R; conversely, the two adults sitting next to S must be F and G.
These two templates provide a powerful insight into the relative placement of the six variables. They also reveal a critical inference! Namely, that H and S must always sit directly across from each other.
Hopefully this convinces you that Circular games, even tiered ones, are hardly the Tenth Circle of hell. We talk about Circular Games in-depth in our In Person and Live Online courses. You can also read about them in our Logic Games Bible in the “Forgotten Few” chapter.


Leave a Reply